- 이 글은 유튜브 Sapientia a Del, 곽기영 교수님, 통계파랑 님을 참고하였습니다.
카이제곱 검정 (교차분석)
- 독립변수와 종속변수 모두 명목척도, 자료의 값은 갯수(count)이어야 함
- 목적
- 변수가 한 개인 경우 : 변수 내 그룹간의 비율이 같은지 다른지
- 그룹이 2개 : binomial test / 이상일 경우 카이제곱
- 변수가 두 개인 경우 : 변수 사이의 연관성이 있는지 없는지 예) 휴대폰 사용과 뇌암의 연관성
$$ \chi^2 = Σ \frac{(O-E)^2}{E},\ df=범주의\ 개수-1 $$
- O (Observed) : 관찰빈도, 데이터에서 자연적으로 주어짐
- E (Expected) : 기대빈도, 별도의 방법으로 구해야
- 예) 고객 데이터에서 특별한 이유가 없는 한, 남/녀 고객의 빈도는 동일하게 나타나야 할 것이라는 가정
- 사실 유의해도 할 이야기가 많지는 않다.
일원 카이제곱 검정
- 한 개의 변수가 명목척도, 2개 이상의 범주를 가짐
예제) payment method라는 변수는 4개의 범주(bank transfer/credit card/electronic check/mailed check). 고객의 지불 방법이 차이가 나는지 알고 싶다면.(각 범주별로 고객의 수가 다를 이유가 없는데 실제로 그런지 알고 싶다, 각 범주별 고객의 수는 비슷할 것이라고가정 )
$$ H_0:P(BT)=P(CC)=P(EC)=P(MC)=0.25,\quad H_a=proportion\ of\ 4\ categories\ are\ not\ even $$
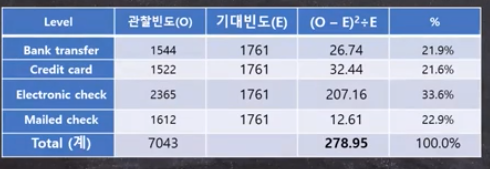
df = 4 - 1 =3
$\chi^2_{df=3}=278.95$
p-value < 0.001
- "다르다" : 사전에 정해진 기대빈도와 다르다.
- 만약 기존의 연구나 혹은 이론 등에 의해서, 각 범주의 빈도가 다르게 나올 수 있다면, 기대빈도 자체를 바꿔서 테스트 해야 함. ⇒ 적합도 (Goodness of fit)
이원 카이제곱 검정
- 두 개의 변수 모두 명목척도, 명목척도는 2개 이상의 범주를 가짐
- 가장 단순한 형태는 $2\times 2$ 분석
- 분할표 (contingency table)사용 : 데이터의 빈도만 단순화 된 표에 작성, 행과 열로 나누어 빈도를 정리 ⇒ 행과 열(두 변수)사이에 어떠한 연관성이 있는지 확인해보는 것
예제) 200명의 암환자 : 진단이 뇌암인지, 휴대폰 사용 3년 이상인지.

- 뇌암환자 72%가 진단 전에 3년 이상 cell phone 사용했다.
P(CP|BC) = 18/25 = 0.72
- 다른 암환자 46%가 진단 전에 3년이상 cell phone 사용했다.
P(CP|NBC) = 80/175 = 0.46
- 이원 카이제곱검정
- 목적 : brain cancer와 cell phone 사용 간의 연관성(인과관계가 아님)
- 가설 : 귀무가설 → 두 사용은 연관성이 없다(상호독립) / 대립가설 → 두 사용간에는 연관성이 있다
- 기대빈도 계산법 : $E=\frac{Row\ Total\ \times\ Column\ Total}{Grand\ Total}$
$$ 12.25 = 98\times 25 /200, \quad 12.75=25\times 102/200,\quad 85.75=98\times175/200,\quad 89.25=102\times 175 / 200$$
$$ \chi^2=\frac{(18-12.25)^2}{12.25}+\frac{(7-12.75)^2}{12.75}+\frac{(80-85.75)^2}{85.75}+\frac{(95-89.25)^2}{89.25}=6.048,\quad df=(2-1)\times(2-1)=1,\quad p-value=0.014$$
⇒ brain cancer와 cell phone 사용 간 어떤 연관성이 있다. 연관성이 인과관계는 아님
→ 범주 간의 확률 차이가 얼마나 큰 지 알 수 없음 ⇒ 신뢰구간 Confidence interval 이용
카이제곱 검정 이외
- 전제조건(한계점)
- 랜덤 샘플링
- 독립성
- 각 범주가 서로 배타적이어야 함
- 한 대상이 하나 이상의 범주에 들어갈 수 없음
- 각 셀의 기대빈도가 5이상이어야 함
- 기대빈도를 5이상으로 맞추기 위해 경우에 따라 범주를 합쳐야 함
- 만약 범주를 합칠 수 없다면, fisher's exact test 나 likelihood ratio test (G-test) 필요
- 만약 df=1?
- 일원 카이제곱 : 범주 2개, 이원 카이제곱 : 2x2인 경우
- 비연속성의 조건부 확률을 연속성의 카이제곱 분포에 적용함으로써 문제 발생 ⇒ 범주의 경우가 너무 적으면 연속성이라는 개념을 충족하기 어려워 짐
- 일원 카이제곱 : yate's correction 또는 chi^2 continuity correction 사용
- 이원 카이제곱 : 카이제곱 테스트와 yate's correction 둘다 하면서 결과가 다르다면 fisher's exact test사용
- $2times 2$의 경우
- 상대 위험도 (Relative Risk)
- 두 확률의 차이인 $P_1 - P_2$ 가 아닌 $P_1 / P_2$ 이용(비율)
- 상대 위험도가 1이라면 두 사건이 발생할 확률은 동일, 1보다 크다면 위험이 증가, 작다면 감소
- 예제) 휴대폰 사용자가 그렇지 않는 사람에 비해 약 2.67배 BC에 걸릴 확률이 높다
- 교차비 / 오즈비
- $Odds = \frac{p}{1-p} $
- 만약 p=3/4, odds=(3/4) / (1/4) = 3 어떤 사건이 일어날 확률이 3/4이라면 오즈는 이사건이 일어나지 않을 확률 대비 일어날 확률은 3배 많다는 것
- 오즈비 : 두 오즈의 비율 $ θ = \frac{\frac{P(A|B)}{1-P(A|B)}}{\frac{P(A|C)}{1-P(A|C}} $
⇒ 오즈비를 사용하면 상대위험도에 비해, 행 열을 바꾸어도 값이 일정하게 나옴
- 예제) P(BC|CP) = P(A|B) = 18/98 = 0.184 / P(BC|NCP) = P(A|C)=7/102=0.069
$$ θ = \frac{\frac{0.184}{0.816}}{\frac{0.069}{0.931}}=\frac{0.225}{0.074}=3.04$$
⇒ BC가 발생할 오즈는 핸드폰 사용자가 그렇지 않은 사람보다 3배 높음
- P(CP|BC) = P(A|B)=18/25 =0.72 / P(CP|NBC)=P(A|C)=80/175=0.457
$$ θ = \frac{\frac{0.72}{0.28}}{\frac{0.457}{0.543}}=\frac{2.57}{0.842} = 3.05$$
⇒ 핸드폰을 가지고 있을 오즈는 BC환자보다 NBC환자가 약 3배 높다
- 오즈비 쉽게 계산하는 방법 $θ = \frac{n_{11}\times n_{22}}{n_{12} \times n_{21}} $
- 두 명목척도인 변수가 연관성이 있을 경우
- 얼마나 상관관계가 높은 지 궁금할 때, 상관계수 구하기 : contingency coefficient, Phi and Cremer's V
- 만약 변수가 순위척도인 경우 연관성이 있다면, 상관계수? : Kendall's tau-b, Gamma
'Today I Learned! > Data Science' 카테고리의 다른 글
| 통계학 (10) - 조절효과와 매개효과 (0) | 2023.12.19 |
|---|---|
| 통계학 (9) - 회귀분석 (0) | 2023.12.13 |
| 통계학 (7) - Three-way ANOVA (0) | 2023.12.10 |
| 통계학 (6) - Repeated Measure ANOVA (0) | 2023.12.06 |
| 통계학 (5) - Contrasts Test (대비검정) (2) | 2023.12.06 |



댓글